Archimedes

Archimedes' Mathematics

What was known before Archimedes?

• Euclid's geometry (fl. c. 300 BC)
• The circumference of a circle is pi times the circle's diameter (definition of pi).  The value of pi was known to be approximately 3.  Until Archimedes arrived, no one had attempted to calculate a more accurate value.
• The area of a circle is a constant (?) times the square of the circle's radius.
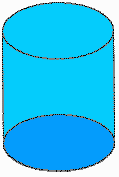
• The volume of a cylinder is the area of the circular base times its height (due to Eudoxus?).

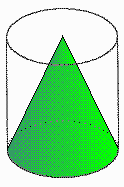
• The volume of a cone is 1/3 of the volume of the cylinder that surrounds it (due to Eudoxus).

Archimedes Traps Pi

Pi is defined as the ratio of the circumference of a circles to its diameter.

(pi as a symbol wasn't used until 1706)

How did Archimedes estimate the value of pi?

He drew two polygons around the circle's center -
one outside the circle (circumscribed) so its perimeter was greater than the circle's,  and
one inside the circle (inscribed) so its perimeter was less than the circle's.

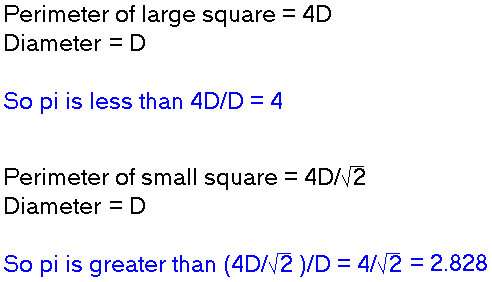
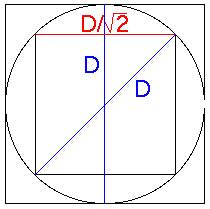
• The more sides the polygons have, the better the estimate of pi.

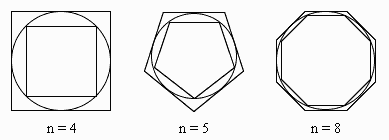
• Archimedes used a polygon with 96 sides to show that the value of pi was between
  3 10/70 and 3 10/71 !

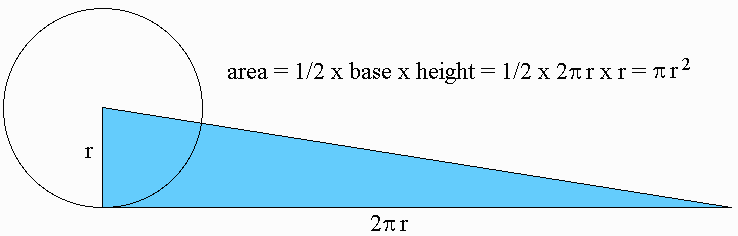
• Using a similar method, Archimedes proved that the area of a circle of diameter D is equal to the area of a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle.

The Recovery of
Archimedes' Method

• In 1899, at the monastery of the Holy Sepulcher at Jerusalem, a 10th-century palimpset was discovered.
• The parchment contained works of Archimedes that, sometime between the 12th and 14th centuries, had been partially erased and overwritten by religious text.
• It included a text of the Method, a work of Archimedes previously thought lost.
• Archimedes used his knowledge of levers and centers of gravity to envision ways of balancing various geometric figures against one another.
• This allowed him to compare their areas or volumes.
• Archimedes then used mathematics to rigorously prove the results of his Method investigations.
  
  "... certain things first became clear to me by a mechanical method, although they had to be proved by geometry afterwards because their investigation by the said method did not furnish an actual proof.  But it is of course easier, when we have previously acquired, by the method, some knowledge of the questions, to supply the proof than it is to find it without any previous knowledge." (from the Method)

Archimedes Discovers the Volume of a Sphere

• Archimedes balanced a cylinder, a sphere, and a cone.  All of the dimensions shown in blue are equal.

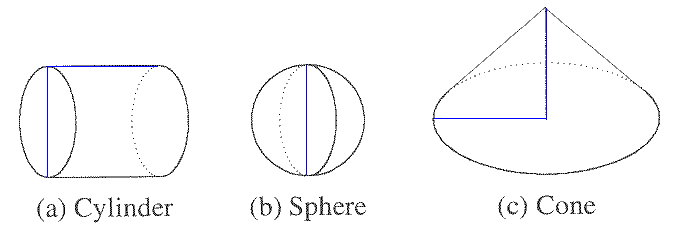
• Archimedes specified that the density of the cone is four times the density of the cylinder and the sphere.

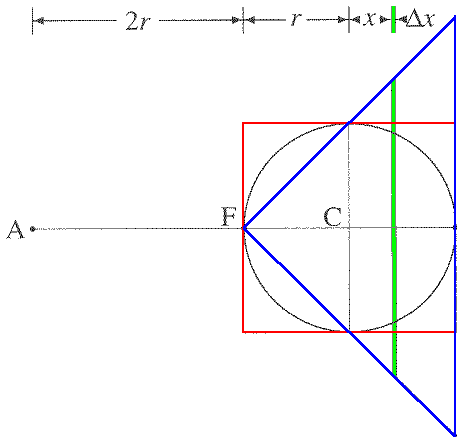
• Archimedes imagined taking a circular slice out of all three solids.
• He then imagined hanging the cylinder and the sphere from point A and suspending the solids at point F (the fulcrum).

• Archimedes showed that the three corresponding slices would always balance, and so the three solids are in balance.
• The cone and sphere at A balance 4 cylinders at C.

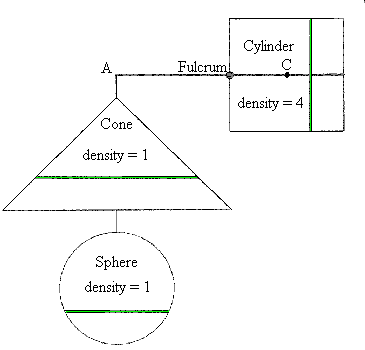
• Using d₁W₁ = d₂W₂ (the law of the lever), Archimedes reasoned that

1 x (cone volume + sphere volume) = 1/2 x (4 cylinder volumes)

• Archimedes already knew the volume of the cylinder and the cone, so he could finally conclude that

sphere volume = 4/3 pi r³

Archimedes knew the volume of a sphere
. . . now he had to prove it!  

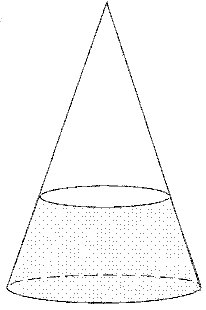
Archimedes built a sphere-like shape from cones and frustrums (truncated cones)

He drew two shapes around the sphere's center -

one outside the sphere (circumscribed) so its volume was greater than the sphere's,  and one inside the sphere (inscribed) so its volume was less than the sphere's.

Here is a example, an inscribed shape made of 2 cones and just 2 frustrums

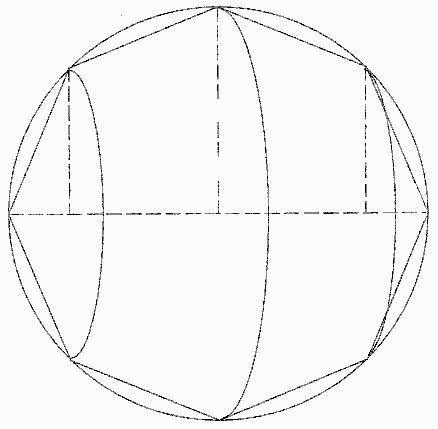
The more frustrums the shape has, the more it looks like a sphere.

This argument allowed Archimedes to rigorously determine
both the volume and surface area of a sphere!

Archimedes' Triumph

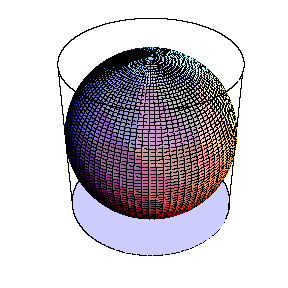
Archimedes stated his result this way:

If a sphere is inscribed in a cylinder,
then the sphere is 2/3 of the cylinder in both surface area and volume.

Archimedes' Greatest Achievement

from Plutarch (AD 45-120), Parallel Lives: Marcellus --

[Archimedes'] discoveries were numerous and admirable; but he is said to have requested his friends and relations that, when he was dead, they would place over his tomb a cylinder containing a sphere, inscribing it with the ratio which the containing solid bears to the contained.

In his dividing of volumes and areas
into the sum of a large number of individual pieces,
Archimedes was essentially using the calculus ---
2000 years before in was developed
by Newton (1643 - 1727) and Leibniz (1646 - 1716)

Another of Archimedes' achievements also used the ideas of the calculus:

• The area of the spiral is 1/3 the area of the circle

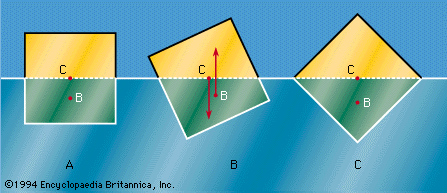
The Father of Hydrostatics

By dividing different shapes into small strips, Archimedes could determine their centers of gravity and buoyancy.  From these he calculated the stability of several different shapes.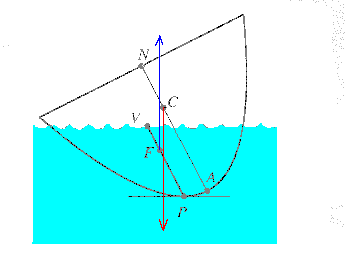

Archimedes at Play

Archimedes wrote about an ancient game that the Greeks called the Stomachion.  He probably did not invent the game, but explored its geometrical aspects. 

The game consisted of 14 flat ivory pieces of various polygonal shapes originally forming a square.  The object of the game was to rearrange the pieces to form interesting things (people, animals, objects, etc.) such as the elephant below.

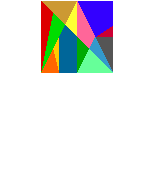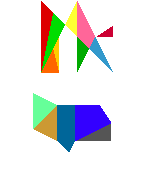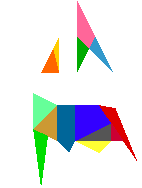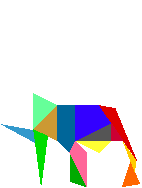
Archimedes and Large Numbers

Archimedes was apparently intrigued by large numbers.  This is his Cattle Puzzle.

"If thou art diligent and wise, O stranger, compute the number of cattle of the Sun, who once upon a time grazed on the fields of the Thrinacian [three-cornered] isle of Sicily, divided into four herds of different colors, one milk white, another a glossy black, a third yellow and the last dappled. In each herd were bulls, mighty in number according to these proportions: Understand, stranger, that the white bulls were equal to a half and a third of the black together with the whole of the yellow, while the black were equal to the fourth part of the dappled and a fifth, together with, once more, the whole of the yellow. Observe further that the remaining bulls, the dappled, were equal to a sixth part of the white and a seventh, together with all of the yellow.  . . ."

The answer contains 206,545 digits!

The first and last fifty digits of the smallest total number of cattle are

77602714064868182695302328332138866642323224059233
. . .

05994630144292500354883118973723406626719455081800 

This problem took 22 centuries and the fastest computers to solve!

The Sand Reckoner

• Greek mathematical notation was not positional; it utilized many symbols and was cumbersome to work with.

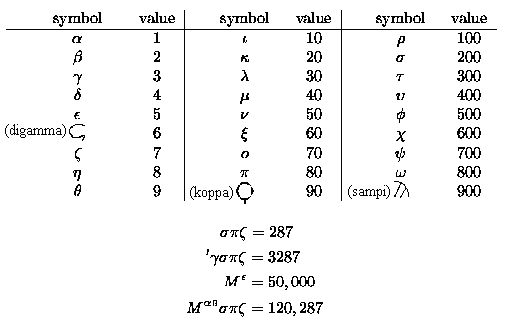
• The "M" is a myriad, and represents 10,000.  The Greek work is murious  (uncountable, pl. murioi).  The Romans converted to this to myriad.
• The Sand Reckoner is a remarkable work in which Archimedes proposes a number system that uses powers of a myriad myriad (base 100,000,000) and is capable of expressing numbers up to 8 x 10⁶³ in modern notation.
• He argues in this work that this number is large enough to count the number of grains of sand
  which could be fitted into the universe.

"There are some, King Gelon, who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited."

"Aristarchus of Samos brought out a book consisting of some hypotheses, in which the premises lead to the result that the universe is many times greater than that now so called.  His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun in the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of the fixed stars, situated about the same center as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the center of the sphere bears to its surface."

Archimedes took Aristarchus to mean that the ratio of the size of the earth to the size of the universe is comparable to that of the orbit of the earth compared to the sphere of stars.

"One can also show that the diameter of the universe is less than a line equal to a myriad diameters of the earth and that, moreover, the diameter of the universe is less than a line equal to one hundred myriad myriad stadia [~ 6 x 10¹² ft, between Saturn and Uranus].  As soon as one has accepted the fact that the diameter of the sun is not greater than thirty moon diameters and that the diameter of the earth is greater than the diameter of the moon, it is clear that the diameter of the sun is less than thirty diameters of the earth."

This was a huge leap over previous estimates of the size of the universe!  Archimedes was the first person to think on the scale of modern astronomy. 

". . . this number is the eighth of the eight numbers, which is one thousand
myriads of eight numbers. . . . It is therefore obvious that the number of grains of sand filling a sphere of the size that Aristarchus lends to the sphere of fixed stars is less than one thousand myriad myriad eighth numbers."

This is Archimedes' estimate of the 8 x 10⁶³ grains of sand to fill the universe.

War Comes to Archimedes

From Plutarch (Greek, c. 45-120 AD) Parallel Lives: Marcellus --

"Archimedes, however, in writing to King Hiero, whose friend and near relation he was, had stated that given the force, any given weight might be moved, and even boasted, we are told, relying on the strength of demonstration, that if there were another earth, by going into it he could remove this. Hiero being struck with amazement at this, and entreating him to make good this problem by actual experiment, and show some great weight moved by a small engine, he fixed accordingly upon a ship of burden out of the king's arsenal, which could not be drawn out of the dock without great labor and many men; and, loading her with many passengers and a full freight, sitting himself the while far off, with no great endeavor, but only holding the head of the pulley in his hand and drawing the cords by degrees, he drew the ship in a straight line, as smoothly and evenly as if she had been in the sea. The king, astonished at this, and convinced of the power of the art, prevailed upon Archimedes to make him engines accommodated to all the purposes, offensive and defensive, of a siege. These the king himself never made use of, because he spent almost all his life in a profound quiet and the highest affluence. But the apparatus was, in most opportune time, ready at hand for the Syracusans, and with it also the engineer himself."

• from Polybius (c. 200 - 118 BC) Universal History --

"The Romans, who had already been informed of the fate which had befallen Hieronymous, the tyrant of Syracuse, appointed . . . Marcus Claudius Marcellus to take charge of the fleet.  . . . The Romans' wicker screens, missiles and other siege apparatus had been made ready beforehand, and they felt confident that with the number of men at their disposal they could within five days bring their preparations to a point which would give them the advantage over the enemy.  But here they failed to reckon with the talents of Archimedes or to foresee that in some cases the genius of one man is far more effective than superiority in numbers. This lesson they now learned by experience."
"The strength of the defenses of Syracuse is due to the fact that the city wall extends in a circle along high ground with steeply overhanging crags, which are by no means easy to climb, except at certain definite points, even if the approach is uncontested.  Accordingly Archimedes had constructed the defenses of the city in such a way - both on the landward side and to repel any attack from the sea - that there was no need for the defenders to busy themselves with improvisations; instead they would have everything ready to hand. . ."
"Archimedes had constructed artillery which could cover a whole variety of ranges, so that while the attacking ships were still at a distance he scored so many hits with his catapults and stone-throwers that he was able to cause them severe damage and harass their approach.  Then, as the distance decreased and these weapons began to carry over the
enemy's heads, he resorted to smaller and smaller machines, and so demoralized the Romans that their advance was brought to a standstill.  In the end Marcellus was reduced in despair to bringing up his ships secretly under cover of darkness.  But when they had almost reached the shore, and were therefore too close to be struck by the catapults, Archimedes had devised yet another weapon to repel the marines, who were fighting from the decks.  He had had the walls pierced with large numbers of loopholes at the height of a man, which were about a palm's breadth wide at the outer surface of the walls.  Behind each of these and inside the walls were stationed archers with rows of so-called 'scorpions', a small catapult which discharged iron darts, and by shooting through these embrasures they put many of the marines out of action."

Archimedes' Claw

From Plutarch (Greek, c. 45-120 AD) Parallel Lives: Marcellus --

"When Archimedes began to ply his engines, he at once shot against the land forces all sorts of missile weapons, and immense masses of stone that came down with incredible noise and violence; against which no man could stand; for they knocked down those
upon whom they fell in heaps, breaking all their ranks and files.  In the meantime huge poles thrust out from the walls over the ships sunk some by the great weights which they let down from on high upon them; others they lifted up into the air by an iron hand or beak

like a crane's beak and, when they had drawn them up by the prow, and set them on
end upon the poop, they plunged them to the bottom of the sea, . . . with great destruction of the soldiers that were aboard them.  A ship was frequently lifted up to a great height in the air (a dreadful thing to behold), and was rolled to and fro, and kept swinging, until the mariners were all thrown out, when at length it was dashed against the rocks, or let fall. Marcellus, doubtful what counsel to pursue, drew off his ships to a safer distance, and sounded a retreat to his forces on land.  They then took a resolution of coming up under the walls, if it were possible, in the night . . . instantly a shower of darts and other missile weapons was again cast upon them. And when stones came tumbling down perpendicularly upon their heads, and, as it were, the whole wall shot out arrows at them, they retired.  And now, again, as they were going off, arrows and darts of a longer range inflicted a great slaughter among them, and their ships were driven one against another; while they themselves were not able to retaliate in any way. For Archimedes had provided and fixed most of his engines immediately under the wall; whence the Romans, seeing that indefinite mischief overwhelmed them from no visible means, began to think they were fighting with the gods." 

"Such terror had seized upon the Romans, that, if they did but see a little rope or a piece of wood from the wall, instantly crying out, that there it was again, Archimedes was about to let fly some engine at them, they turned their backs and fled, Marcellus desisted from conflicts and assaults, putting all his hope in a long siege."

• After a year of effort, Marcellus' siege was eventually successful in 212/211 BC.
  
   
• Syracuse may have been betrayed when the citizens went in a body to Marcellus, or perhaps it was plundered by the Romans while the citizens were keeping a night festival to Artemis (daughter of Zeus).
  
  

From Plutarch (Greek, c. 45-120 AD) Parallel Lives: Marcellus --

"But nothing afflicted Marcellus so much as the death of Archimedes, who was then, as fate would have it, intent upon working out some problem by a diagram, and having fixed his mind alike and his eyes upon the subject of his speculation, he never noticed the incursion of the Romans, nor that the city was taken.  In this transport of study and contemplation, a soldier, unexpectedly coming up to him, commanded him to follow to Marcellus; which he declining to do before he had worked out his problem to a demonstration, the soldier, enraged, drew his sword and ran him through.  . . . Certain it is that his death was very afflicting to Marcellus; and that Marcellus ever after regarded him that killed him as a murderer; and that he sought for his kindred and honored them with signal favors."

A Question to Ponder

• After Archimedes death, 2000 years would pass before a comparable mathematical figure arises.
• In quick succession came Descartes (1596 - 1650), Fermat (1601 - 1665), Pascal (1623 - 1662), Newton (1642 - 1727), Leibniz (1646 - 1716), and Euler (1707 - 1789).
• What happened between Archimedes and Descartes?

Alfred North Whitehead (1861-1947), An Introduction to Mathematics --

"The death of Archimedes by the hands of a Roman soldier is symbolical of a world-change of the first magnitude: the Greeks, with their love of abstract science, were superseded in the leadership of the European world by the practical Romans.  The Romans were a great race, but they were cursed with the sterility which waits upon practicality. They did not improve upon the knowledge of their forefathers, and all their advances were confined to the minor technical details of engineering. They were not dreamers enough to arrive at new points of view, which could give a more fundamental control over the forces of nature. No Roman lost his life because he was absorbed in the contemplation of a mathematical diagram."